이진탐색트리, AVL트리
이진탐색트리는 binary search와 linked list를 결합한 자료구조이다. 이진 탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제를 가능하게끔 고안되었다. 이진탐색의 경우 탐색에
the-ze.tistory.com
Red/Black Tree Visualization
www.cs.usfca.edu
레드 블랙 트리는 이진 탐색트리의 한 종류로써, 스스로 균형을 잡는 트리이다. BST의 worst case의 단점 O(N)을 개선했다. 이 레드 블랙 트리에는 몇 가지 규칙들이 있다.
1. 모든 노드는 red 혹은 black
2. 최상위 루트 노드는 black
3. 모든 nil(leaf) 노드는 black
4. red의 자녀들은 black (red가 연속적으로 존재할 수 없다.)
5. 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다. (자기 자신은 카운트에서 제외)
여기서 nil 노드란?
1. 존재하지 않음을 의미하는 노드
2. 자녀가 없을 때 자녀를 nil 노드로 표기 (nil이 있다면 자녀가 없는 것을 의미)
3. 값이 있는 노드와 동등하게 취급
4. RB트리에서 leaf노드는 nil 노드
5. 모든 nli 노드는 black

RB 트리가 위 속성을 만족하고 있고 두 자녀가 같은 색을 가질 때 부모와 두 자녀의 색을 바꿔줘도 속성은 여전히 만족한다.

RB트리는 주로 삽입/삭제할 때 균형을 맞춘다.
red의 자녀들은 black , red가 연속적으로 존재할 수 없다.
임의의 노드에서 자손 nil노드들까지 가는 경로들의 black의 수는 같다.
이 둘을 위반하며 이들을 해결하려고 구조들 바꾸다 보면 자연스럽게 트리의 균형이 잡히게 된다.
삽입 방식
1. 삽입 전 RB트리 속성 만족한 상태
2. 삽입 방식은 일반적인 BST와 동일
3. 삽입 후 RB트리 위반 여부 확인
4. RB트리 속성을 위반했다면 재조정
5. RB트리 속성을 다시 만족
삽입하는 노드의 색깔은 항상 red이다.
node_t *rbtree_insert(rbtree *t, const key_t key)
{
// TODO: implement insert
// 적절한 위치 찾는 코드
// 값 삽입
node_t *SENTINEL_NODE = t->nil;
node_t *parent_node = t->nil;
node_t *new_node = malloc(sizeof(node_t));
new_node->key = key;
new_node->right = SENTINEL_NODE;
new_node->left = SENTINEL_NODE;
new_node->color = RBTREE_RED;
node_t *cur_node = t->root;
while (cur_node != SENTINEL_NODE)
{
parent_node = cur_node;
if (cur_node->key > key)
{
cur_node = cur_node->left;
}
else
{
cur_node = cur_node->right;
}
}
new_node->parent = parent_node;
if (parent_node == SENTINEL_NODE)
{
t->root = new_node;
}
else if (new_node->key < parent_node->key)
{
parent_node->left = new_node;
}
else
{
parent_node->right = new_node;
}
rbtree_insert_fixup(t, new_node);
return new_node;
}
일반적인 삽입만 했다면, 맨 위의 5가지 규칙이 깨지지 때문에 이를 규칙에 맞게 다시 재조정할 필요가 있다.
위의 시뮬레이터로 계속 삽입을 하면 보이다 싶이, 결국 black 노드가 많아지는 것을 볼 수가 있다.
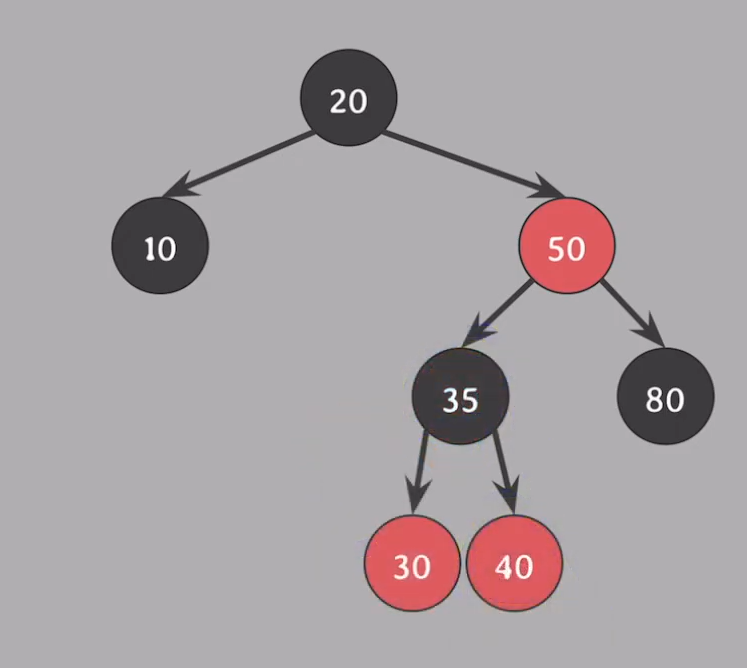
위 사진에서 insert(25)를 해보자.
그럼 30의 좌측 자식 red노드로 처음엔 삽입될 것 이다. 이는 5가지 규칙 중 노드가 red라면 자녀들은 black을 위반한 상태이다. 부모와 삼촌을 black으로, 할아버지는 red로 변경하고 할아버지인 35에서 확인해보자 50 > 35가 레드가 되니 노드가 red라면 자녀들은 black을 위반한 상태이다. 그러면 50을 기준으로 오른쪽으로 회전해보자

그러면 또 35와 50을 보면 문제가 생기는데, 20과 35의 색깔을 바꿔주고 20을 기준으로 왼쪽으로 회전하면 된다.

구현할 때, 이런 재조정에 신경을 쓰며 구현을 해야한다.
void rbtree_insert_fixup(rbtree *t, node_t *p)
{
while (p->parent->color == RBTREE_RED)
{
if (p->parent == p->parent->parent->left)
{
node_t *y = p->parent->parent->right;
if (y->color == RBTREE_RED)
{
p->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
p->parent->parent->color = RBTREE_RED;
p = p->parent->parent;
}
else
{
if (p == p->parent->right)
{
p = p->parent;
left_rotate(t, p);
}
p->parent->color = RBTREE_BLACK;
p->parent->parent->color = RBTREE_RED;
right_rotate(t, p->parent->parent);
}
}
else
{
node_t *y = p->parent->parent->left;
if (y->color == RBTREE_RED)
{
p->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
p->parent->parent->color = RBTREE_RED;
p = p->parent->parent;
}
else
{
if (p == p->parent->left)
{
p = p->parent;
right_rotate(t, p);
}
p->parent->color = RBTREE_BLACK;
p->parent->parent->color = RBTREE_RED;
left_rotate(t, p->parent->parent);
}
}
}
t->root->color = RBTREE_BLACK;
}
삭제하려는 노드의 *자녀가 없거나 하나라면 삭제되는 색 = 삭제되는 노드의 색
삭제하려는 노드의 자녀가 둘이라면 삭제되는 색 = 삭제되는 노드의 successor
삭제되는 색이 red라면 어떠한 속성도 위반하지 않는다.
int rbtree_erase(rbtree *t, node_t *p)
{
node_t *target_node = p;
node_t *x;
color_t target_node_orginal_color = target_node->color;
if (p->left == t->nil)
{
x = p->right;
rbtree_erase_transplant(t, p, p->right);
}
else if (p->right == t->nil)
{
x = p->left;
rbtree_erase_transplant(t, p, p->left);
}
else
{
target_node = node_min(p->right, t->nil);
target_node_orginal_color = target_node->color;
x = target_node->right;
if (target_node->parent == p)
{
x->parent = target_node;
}
else
{
rbtree_erase_transplant(t, target_node, target_node->right);
target_node->right = p->right;
target_node->right->parent = target_node;
}
rbtree_erase_transplant(t, p, target_node);
target_node->left = p->left;
target_node->left->parent = target_node;
target_node->color = p->color;
}
if (target_node_orginal_color == RBTREE_BLACK)
rbtree_erase_fixup(t, x);
free(p);
return 0;
}
10을 삭제시키면 임의의 노드에서 그 노드의 자손 nil노드들까지 가는 경로들의 black 수는 같다를 위반한다.

삭제된 10에 extra black을 부여해야한다. 근데 삭제하고 넣을 때 그 사이에 nil노드가 생겨버리기 때문에, 블랙이 두개가 생겨버린다. 이를 doubly black이라고 한다.

rb tree의 삭제는 해당 노드를 삭제하고 extra black을 부여 후, doubly black만 잘 해결하면 된다. 이를 해결하는 방법에는 4가지 case가 있다.
1. doubly black의 오른쪽 형제가 black이고, 그 형제의 오른쪽 자녀가 red일 때
2. doubly black의 오른쪽 형제가 black이고, 그 형제의 왼쪽 자녀가 red일 때
3. doubly black의 오른쪽 형제가 black이고, 그 형제의 두 자녀가 모두 black 일 때
4. doubly black의 오른쪽 형제가 red일 때
(위 모든 케이스 오른쪽, 왼쪽을 바꾼 상황이여도 적합함)
이 케이스들에 유의하며 코드를 짜야한다.
void rbtree_erase_fixup(rbtree *t, node_t *fixup_start_node)
{
node_t *cur_node = fixup_start_node;
node_t *sibling;
while (cur_node != t->root && cur_node->color == RBTREE_BLACK)
{
if (cur_node == cur_node->parent->left)
{
sibling = cur_node->parent->right;
if (sibling->color == RBTREE_RED)
{
sibling->color = RBTREE_BLACK;
cur_node->parent->color = RBTREE_RED;
left_rotate(t, cur_node->parent);
sibling = cur_node->parent->right;
}
if (sibling->left->color == RBTREE_BLACK && sibling->right->color == RBTREE_BLACK)
{
sibling->color = RBTREE_RED;
cur_node = cur_node->parent;
}
else {
if (sibling->right->color == RBTREE_BLACK)
{
sibling->left->color = RBTREE_BLACK;
sibling->color = RBTREE_RED;
right_rotate(t, sibling);
sibling = cur_node->parent->right;
}
sibling->color = cur_node->parent->color;
cur_node->parent->color = RBTREE_BLACK;
sibling->right->color = RBTREE_BLACK;
left_rotate(t, cur_node->parent);
cur_node = t->root;
}
}
else {
sibling = cur_node->parent->left;
if (sibling->color == RBTREE_RED)
{
sibling->color = RBTREE_BLACK;
cur_node->parent->color = RBTREE_RED;
right_rotate(t, cur_node->parent);
sibling = cur_node->parent->left;
}
if (sibling->left->color == RBTREE_BLACK && sibling->right->color == RBTREE_BLACK)
{
sibling->color = RBTREE_RED;
cur_node = cur_node->parent;
}
else
{
if (sibling->left->color == RBTREE_BLACK)
{
sibling->right->color = RBTREE_BLACK;
sibling->color = RBTREE_RED;
left_rotate(t, sibling);
sibling = cur_node->parent->left;
}
sibling->color = cur_node->parent->color;
cur_node->parent->color = RBTREE_BLACK;
sibling->left->color = RBTREE_BLACK;
right_rotate(t, cur_node->parent);
cur_node = t->root;
}
}
}
cur_node->color = RBTREE_BLACK;
}
GitHub - RB-TREE-TEAM7/rbtree-lab
Contribute to RB-TREE-TEAM7/rbtree-lab development by creating an account on GitHub.
github.com
'CS > 자료구조' 카테고리의 다른 글
| B-tree, B+tree, Trie, Minimum Spanning Tree (1) | 2024.04.01 |
|---|---|
| Graph, Adjacency Matrix, Adjacency List (0) | 2024.03.31 |
| Hash Table (collision, chaining, rehashing) (1) | 2024.03.31 |
| Array, Linked List (2) | 2024.03.28 |
| 이진탐색트리, AVL트리 (0) | 2024.03.21 |