이진탐색트리는 binary search와 linked list를 결합한 자료구조이다. 이진 탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제를 가능하게끔 고안되었다.
이진탐색의 경우 탐색에 소요되는 계산 복잡성은 O(logN)으로 빠르지만 자료 입력, 삭제가 불가능하다. 연결 리스트의 경우에는 자료 입력, 삭제에 필요한 계산복잡성은 O(1)로 효율적이지만, 탐색하는 데에는 O(n)의 계산 복잡성이 발생한다.
- 각 노드의 왼쪽 서브트리에는 해당 노드의 값보다 작은 값을 지닌 노드들로 이루어져 있다.
- 각 노드의 오른쪽 서브트리에는 해당 노드의 값보다 큰 값을 지닌 노드들로 이루어져 있다.
- 중복된 노드가 없어야 한다.
- 왼쪽 서브트리, 오른쪽 서브트리 또한 이진탐색트리이다.

이진탐색트리를 순회할 때는 중위순회(inorder) 방식을 쓴다. (왼쪽 서브트리-노드-오른쪽 서브트리 순으로 순회) 중위순회 방식을 사용하면 이진탐색트리 내에 있는 모든 값들을 정렬된 순서대로 읽을 수 있다. (1,5,6,10,14,17,21)
이진탐색트리의 핵심 연산은 검색, 삽입, 삭제 세 가지이다. 이밖에 이진탐색트리 생성, 이진탐색트리 삭제, 해당 이진탐색트리가 비어 있는지 확인, 트리순회 등의 연산이 있다.
탐색(검색)
이진탐색트리의 탐색 연산에 소요되는 계산복잡성은 트리의 높이(루트노드-잎새노드에 이르는 엣지 수의 최대값)가 h일 때 O(h)가 된다.
삽입
트리가 매우 적으면 그냥 중간에 삽입하면 되는데, 매우 길어질 때를 방지하기 위하여, 새로운 삽입은 무조건 리프노드에서 이루어지게된다. 삽입 연산에 소요되는 계산복잡성 역시 트리의 높이가 h일 때 O(h)이다. 삽입할 위치의 리프노드까지 찾아 내려가는 데 h번 비교를 해야 하기 때문이다.
삭제할 때의 경우
- 자식노드가 없는 경우 - 그냥 삭제하면 된다.
- 자식노드가 하나 있는 경우 - 본인을 삭제하고 부모와 자식을 연결하면 된다.
- 자식노드가 두 개 있는 경우 - 아래 과정을 따른다.
자식노드가 두 개 있을 때 삭제 과정
- 삭제 대상 노드의 오른쪽 서브트리를 찾는다.
- successor 노드를 찾는다.
- 2에서 찾은 successor의 값을 삭제 대상 노드에 복사한다.
- successor 노드를 삭제한다.
successor란? 중위 순회를 나열한 배열에서 본인의 바로 다음에 있는 노드이다. 즉 본인보다 오른쪽에 있으면서, 가장 작은 노드이다. (맨위 사진에서 [1,5,6,10,14,17,21] 여기서 10의 successor는 14이다.)

17 우측에 있는 노드 중에 가장 작은 19가 successor이다.
트리의 높이가 h이고 삭제 대상 노드의 레벨이 n라고 가정할 때, 1번 과정에서는 n번의 비교 연산이 필요하다. 2번 successor 노드를 찾기 위해서는 삭제 대상 노드의 서브트리 높이(h-d)에 해당하는 비교 연산을 수행해야 한다. 3번 4번은 복사하고 삭제하는 과정으로 상수시간이 걸려 무시할 만 하다. 종합적으로 따지면 O(d+h-d), 즉 O(h)가 된다.
노드가 루트의 한쪽으로 쏠려버리면 균형이 안맞아서 비효율적이다. 그러면 O(n)이 되는데 이를 해결하기 위해 균형을 맞추는 AVL Tree가 고안되었다.
AVL 트리는 편향된 트리의 균형을 맞추기 위한 트리이다.
- 이진 탐색 트리의 속성을 가진다.
- 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
- 높이 차이가 1보다 커지면 회전(Rotation)을 통해 균형을 맞춰 높이 차이를 줄인다.
- 삽입, 검색, 삭제의 시간 복잡도가 O(log N)이다. (N : 노드의 개수)
회전 과정에 대해 알아보기 전에 알아야 할 것이있다. AVL트리는 균형이 무너졌는지에 대해 판단할 때 Balance Factor라는 것을 활용한다. 이는 아래와 같은 공식으로 구한다.
BF(K) = K의 왼쪽 서브트리의 높이 - K의 오른쪽 서브트리의 높이
우회전
1. y노드의 오른쪽 자식 노드를 z노드로 변경한다.
2. z노드 왼쪽 자식 노드를 y노드의 오른쪽 서브트리(T2)로 변경한다.
좌회전
1. y노드의 왼쪽 자식 노드를 z노드로 변경한다.
2. z노드 오른쪽 자식노드를 y노드의 왼쪽 서브트리(T2)로 변경한다.
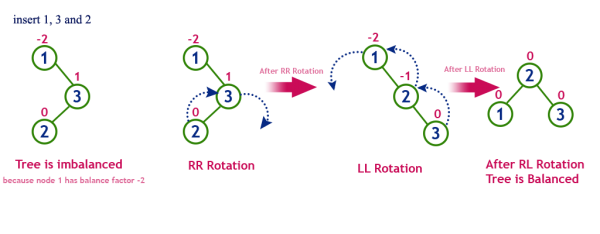
Case를 기준으로 트리의 균형을 맞춘다.
LL Case일 때 해당 노드 기준 우회전

RR Case일 때 해당 노드 기준 좌회전

LR Case왼쪽 자식노드 기준으로 좌회전 히고 해당 노드 기준 우회전

RL Case오른쪽 자식노드 기준으로 우회전 하고 해당 노드 기준 좌회전
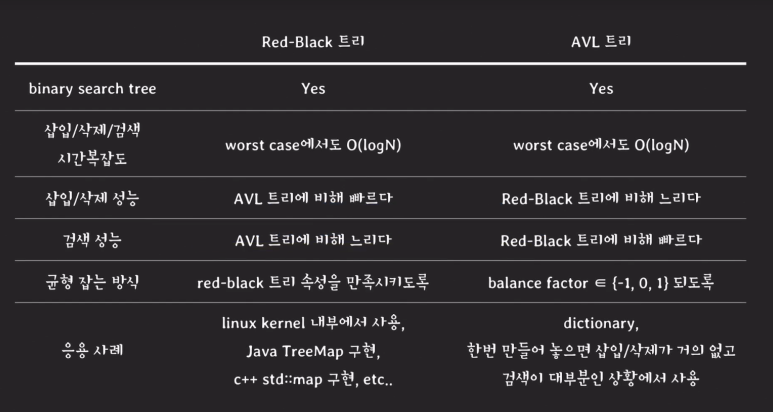
AVL트리는 이진 탐색트리의 균형을 맞출 뿐, 삽입 삭제는 비효율적이기 때문에, Dictionary 같은 잘 변동이 없는 것을 구현할 때 주로 사용되고, 삽입 삭제를 효율적으로 하기 위해 고안된 트리가 바로 RB트리이다.
RB트리 : https://the-ze.tistory.com/entry/Red-Black-Tree-%EA%B5%AC%ED%98%84
Red-Black Tree 구현
이진 탐색 트리, AVL트리: https://the-ze.tistory.com/entry/%EC%9D%B4%EC%A7%84%ED%83%90%EC%83%89%ED%8A%B8%EB%A6%AC-AVL%ED%8A%B8%EB%A6%AC 이진탐색트리, AVL트리 이진탐색트리는 binary search와 linked list를 결합한 자료구조이다.
the-ze.tistory.com
Binary Search Tree 구현 (yunsejin 폴더에 있음)
GitHub - yunsejin/Data-Structure-C-Language-Exercises
Contribute to yunsejin/Data-Structure-C-Language-Exercises development by creating an account on GitHub.
github.com
'CS > 자료구조' 카테고리의 다른 글
| B-tree, B+tree, Trie, Minimum Spanning Tree (1) | 2024.04.01 |
|---|---|
| Graph, Adjacency Matrix, Adjacency List (0) | 2024.03.31 |
| Hash Table (collision, chaining, rehashing) (1) | 2024.03.31 |
| Array, Linked List (2) | 2024.03.28 |
| Red-Black Tree 구현 (0) | 2024.03.22 |